In the movie “Ship Ahoy”, Eleanor Powell’s character tap dances as message in Morse code.
In real life, Vietnam POW Jeremiah Denton informed the world that prisoners were being tortured by blinking out the word “TORTURE” in Morse code.
I cannot be denied that Morse code is useful.
It is not the easiest system to master, however.
You have doubtless seen movies where someone knocks on the plumbing and a character identifies it as Morse code, which one of them can understand.
Morse code actually requires two signals, distinct in sound or duration, so it is impossible to tap out certain characters in Morse by banging on pipes.
SOS is one of the few signals you can tap out with a single sound. In this instance you may vary the interval between taps, rather than their duration. Three fast taps, three slow taps, three fast.
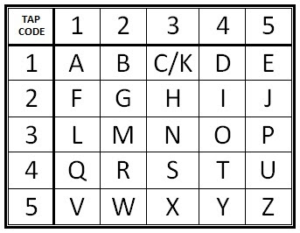
Another code system used by POWs was the tap code, sometimes known as the 5 by 5 tap code.
This code relies on creating or visualizing a 5 x 5 table of letters.
C and K are treated as the same letter.
The position of the desired letter in the matrix is identified by two sequences of between one and five knocks.
For the first set of knocks you count down the rows of the matrix.
For the second set you count across the columns.
Three knocks in the first sequence would have you count down to “L”.
Four following knocks would have you count across and end on “O”.
3-4 is therefore “O”.
A disadvantage of this code is that more than half the alphabet requires six or more knocks. Common letters such as U and Y need nine!

An idea that occurs to me is to combine some elements of Morse and the Tap code.
To do this, the references for the letters are converted into binary, using “dits” for zeros and “dahs” for ones.
A number value up to seven can be represented by a three-figure binary number.
The location of any letter on the Tap code matrix can therefor be represented by six figures or six taps.
That all letters are the same length may be useful for some applications such as binary one-use pads.
Since “O” is 3-4 it can be represented as 011-100 or dit-dash-dash-dash-dit-dit.
A dash means to move down a row or across a column, a dit to stay.
The binary system also allows us to distinguish “K”. Logically this is to the right of “J” so 010-110.
The binary referenced table potentially has 49 character positions, 64 if the zero rows and columns are included.
Numerals zero to five would be 000-000 to 000-101. Six to nine would be 001-000, 010-000, 011-000 to 100-000.
This is similar to the hand signals for numerals six to nine. 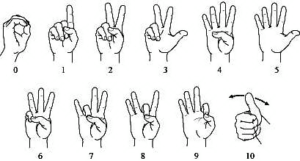

SOS would be 100-011, 011-100, 100-011, so the Morse code …—… is easier to retain.
In binary tap code this effectively 3-7-3.
None of the standard letters use 7 so seven on its own could be used as a distress or “!”.